虚数がよくわかる:“ありもしない”のに,難問解決に不可欠な数(Newton別冊) [本(数学]
 『虚数がよくわかる』
『虚数がよくわかる』木村俊一(代数幾何)
Newton別冊(2009)
訳語の虚数は中国で作られた
虚数は数直線に対して垂直方向の矢印
iの四乗が1
虚数同士には大小はない
シュレーディンガー方程式は虚数を含む
ホーキング:宇宙のはじまりには虚数の時間が存在したが、
やがて実数の時間に置きかわった。
虚数時間のもとでは力の向きが逆転する
宇宙のはじまりに虚数時間を想定すれば、
そこでは時間と空間がまったく対等なものになり、両者の区別がなくなる。
虚数はもちろんマイナスもゼロも自然界には存在しない
商人がサファイアを520ダカットで売った。
仕入れ値は、もうけのちょうど3乗に等しかったという。もうけはいくらか?
複素数こそ、数の拡張の終着駅であり、これ以上の数の拡張は必要ない
一個の実数と3個の虚数からなる新しい数:四元数=ハミルトン数
黄金比の美しさは幻想
☆☆☆☆☆
数学の本の問題は、
数式の計算部分を完全に書き出さないことだと思う。
数語の完全翻訳本を書く数学ライターはいないのかな?
たとえば、
メソポタミア人はどうやって求めた?
の解説は、以下ぐらいに徹底して書くべきと思う。
古代メソポタミア人はどのようにして√2の近似値を求めたのだろうか?
2は、「1の2乗(=1)]よりは大きいが、「2の2乗(=4)」よりは小さい。したがって、√2は「1と2の間」に存在することがわかる。もし、1と2の中間値である3/2=1.5が√2そのものであれば、(2÷3/2)の計算結果も3/2になるはずである。だが実際には2÷3/2=4/3=1.3333…となるので、√2は「4/3と3/2の間」に存在することがわかる。
そこで、今度は4/3と3/2の中間値である17/12=1.41666…を新たな√2候補とし、これを2で割ると、2÷17/12=24/17=1.41176…となるので、√2は「24/17と17/12の間」に存在することがわかる。メソポタミア人はこうした計算をくりかえすことで、より正確な近似値を求めることができたと考えられている。
・今日の一言(本文より)
2乗してマイナスになる数さえあれば、どんな2次方程式にも答えが出せる。
제곱해서 마이너스가 되는 숫자만 있으면 어떤 2차 방정식에도 답이 나올 수 있다.
要是有二次平方后得出负数的数字,那么不论什么二次方程式都能解答。
If you have a number which turns into a negative number when it is squared, you can answer any quadratic equation.
タグ:木村俊一
 光武帝チート伝説(だがすべて史実である)
光武帝チート伝説(だがすべて史実である) アンジャッシュに学ぶユーモアの方程式
アンジャッシュに学ぶユーモアの方程式 経済学批判:経済学に不足する4つの視点
経済学批判:経済学に不足する4つの視点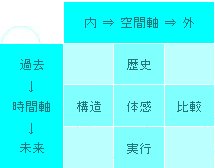 5種類の論理の方法
5種類の論理の方法 三大学習英英辞典(オックスフォード、ロングマン、コウビルド)の比較
三大学習英英辞典(オックスフォード、ロングマン、コウビルド)の比較 英語、中国語、韓国語、日本語の発音の違いとコツ。
英語、中国語、韓国語、日本語の発音の違いとコツ。 浄土仏教の科学的解釈
浄土仏教の科学的解釈 ●洋書を読もう!
・SHARP Brain(ブレーン) カラー液晶電子辞書 スタイリッシュモデル 12コンテンツ グリーン系 PW-AC10-G
●洋書を読もう!
・SHARP Brain(ブレーン) カラー液晶電子辞書 スタイリッシュモデル 12コンテンツ グリーン系 PW-AC10-G ●中国語を極める
・カシオEX-word 電子辞書 中国語モデル XD-N7300WE ホワイト
●中国語を極める
・カシオEX-word 電子辞書 中国語モデル XD-N7300WE ホワイト ●韓国語を極める
・カシオEX-word 電子辞書 韓国語モデル XD-N7600
●韓国語を極める
・カシオEX-word 電子辞書 韓国語モデル XD-N7600 ●英語を極める
・セイコーインスツル 電子辞書 DAYFILER デイファイラー DF-X10000 日本語・英語プロフェッショナル向け 無線LAN搭載モデル
●英語を極める
・セイコーインスツル 電子辞書 DAYFILER デイファイラー DF-X10000 日本語・英語プロフェッショナル向け 無線LAN搭載モデル ●日本語を極める
・カシオEX-word 電子辞書 プロフェッショナルモデル XD-N10000
●日本語を極める
・カシオEX-word 電子辞書 プロフェッショナルモデル XD-N10000 ●医学を極める
・セイコーインスツル 電子辞書 DAYFILER デイファイラー DF-X11000 医学用電子辞書 無線LAN搭載モデル
●医学を極める
・セイコーインスツル 電子辞書 DAYFILER デイファイラー DF-X11000 医学用電子辞書 無線LAN搭載モデル
コメント 0